从零开始造一台自己的加法器
在电子学中,加法器(adder)是一种用于执行加法运算的数字电路部件,是构成电子计算机核心微处理器中算术逻辑单元的基础。在这些电子系统中,加法器主要负责计算地址、索引等数据。除此之外,加法器也是其他一些硬件的重要组成部分。
10 进制与 2 进制
10 的替代品
对我们人类而言,10 是一个非常重要的数字。10 是我们大多数人拥有的手指或脚趾的数目,因为手非常便于计数,于是我们已经适应了这个以 10 为基数的数字系统。起初也很难再构想出其它的数字系统。

当我们看到数字 10 的时候,我们不自觉地就想到这个数字代表了下面的这么多个苹果:
10 =
但是,数字 10 之所以指的是这么多个苹果,其唯一的理由就在于这些苹果的数目与我们手指的数目相同。如果人类的手指不是 10 根,我们数数的方式就会有所不同,那么 10 就会是另外一个含义。
同样,数字 10 还可以代表这么多个苹果:
10 =
或者是这么多个苹果:
10 =
甚至可以是这么多个苹果:
10 =
设想一下: 如果人类像卡通人物一样每只手有 4 根手指那会怎样呢?

我们可能就不会想到建立一个以 10 为基数的数字系统。我们会自然而然地、不可避免地想到建立一个以 8 为基数的数字系统。我们会称它为八进制数字系统。如果我们的数字系统是以 8 为基数而建立的,我们就不需要下面这个符号:
9
将这个给卡通人物看的话,他会得到这样的反应:”这是什么?它代表什么?“ 继续思考一下,你会发现我们连这样的一个符号也不会需要:
8
在十进制中,”十”没有特定的符号,因此在八进制中,同样也没有表示”八”的特定符号。
十进制中我们的计数方式是:0、1、2、3、4、5、6、7、8、9,然后是 10。
八进制中我们的计数方式是:0、1、2、3、4、4、5、7,然后是什么呢?我们已经将符号用完了。在这里唯一有意义的只有 10,而在这里的正确答案恰恰就是 10。在八进制中,7 之后的一个数字就是 10。但这个 10 代表的并不是人类的手指的数量。在八进制中,10 代表的是卡通人物手指的数量。
2 进制
如果我们是海豚呢,那么就必须用两个鳍来计数。这个数字系统称为以 2 为基数的数字系统。这样的话我们似乎只有两个数字了,分别为 0 和 1。在二进制中,1 的下一个数字是 10。第一次见似乎有点难以理解,但也不用意外。因为无论使用哪种计数系统,当单个的数字用完时,第一个两位数就是 10。

二进制数最大的问题是数字用完的很快!
0,1,10,11,100,101,110,111,1000,1001,1010,1011,1100,1110,1111,10000,10001,…
当然,二进制也有它的优点,比如做加法的时候:
11 加法表
| + | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 10 |
乘法比加法还容易,比起小时候背的 99 乘法表 不知道简单了多少。
11 乘法表
| x | 0 | 1 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
99 乘法表
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | ||||||||
| 2 | 2 | 4 | |||||||
| 3 | 3 | 6 | 9 | ||||||
| 4 | 4 | 8 | 12 | 16 | |||||
| 5 | 5 | 10 | 15 | 20 | 25 | ||||
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | |||
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | ||
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 |
电磁铁与继电器
电磁铁
如果你手头有一根铁棒,那么在上面用细导线绕几百圈,然后接通电流,铁棒就变成了一块磁铁。现在它可以吸引其它的铁块或者钢块(电磁铁上缠绕足够多的细导线,会产生足够强的电阻,能防止电磁铁产生短路现象)。断开电流,铁棒将丧失磁性。
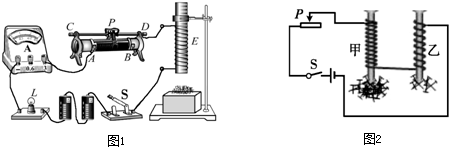
图1 中的电路组成元件按顺时针方向依次是
- ABCDP 滑动变阻器
- E 电磁铁
- S 单刀单掷开关
- 电池
- L 电灯泡
- 电流表
继电器
继电器的作用就是通过吸引或弹开衔铁,进而控制另一个电路的通断。
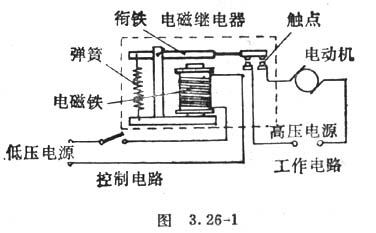
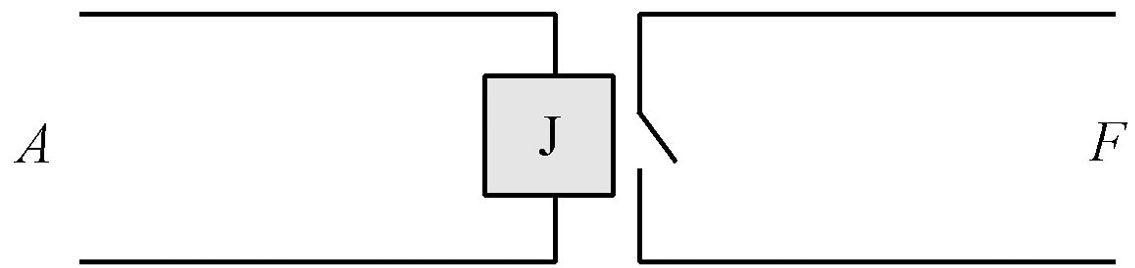
继电器符号和电路图如下所示:
门
非门
结果与操作数相反。
真值表
| NOT | 0 | 1 |
|---|---|---|
| 1 | 0 |
符号
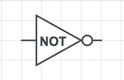
电路图
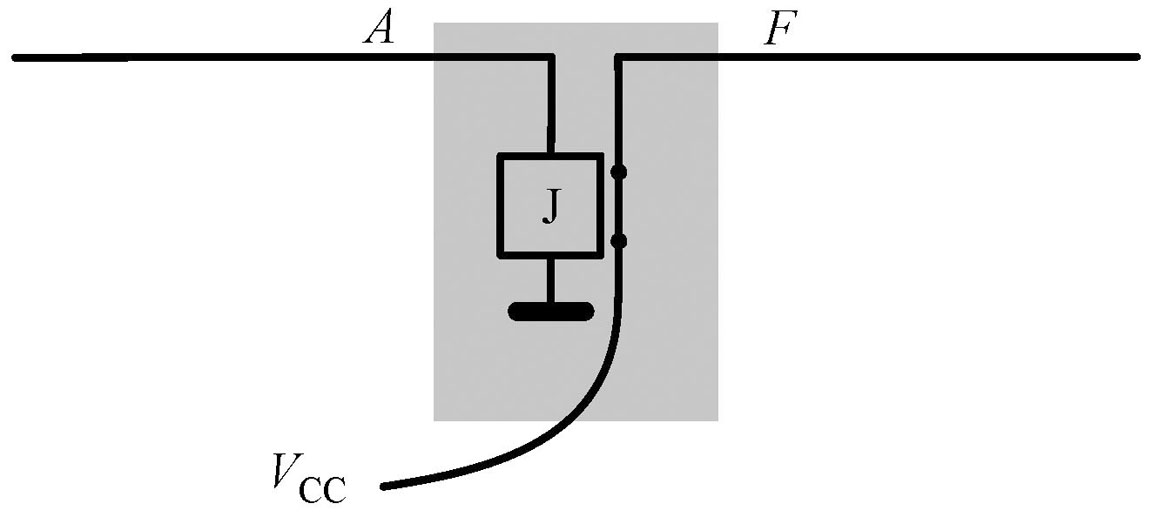
与门
两个操作数都为 1 时结果为 1。
真值表
| AND | 0 | 1 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
符号
电路图
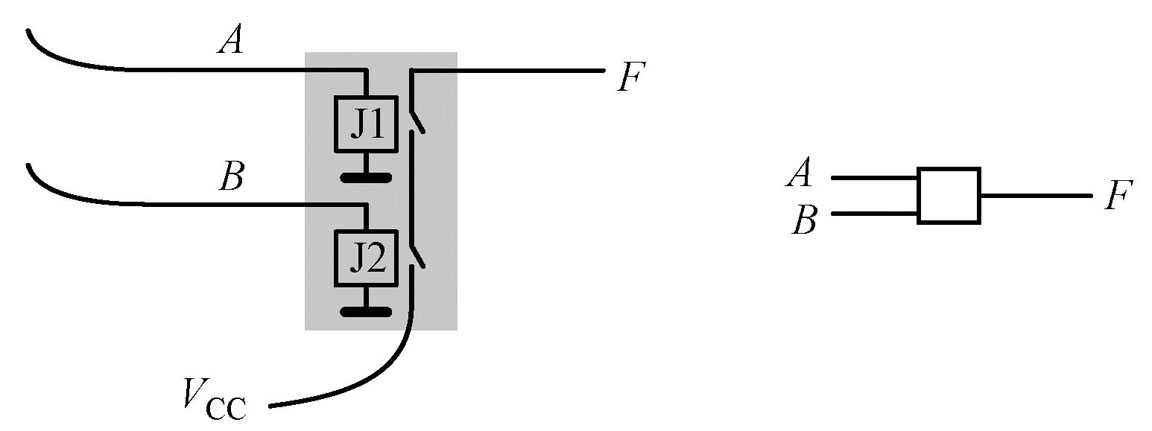
或门
有一个操作数为 1 结果就为 1。
真值表
| OR | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 1 |
符号
电路图
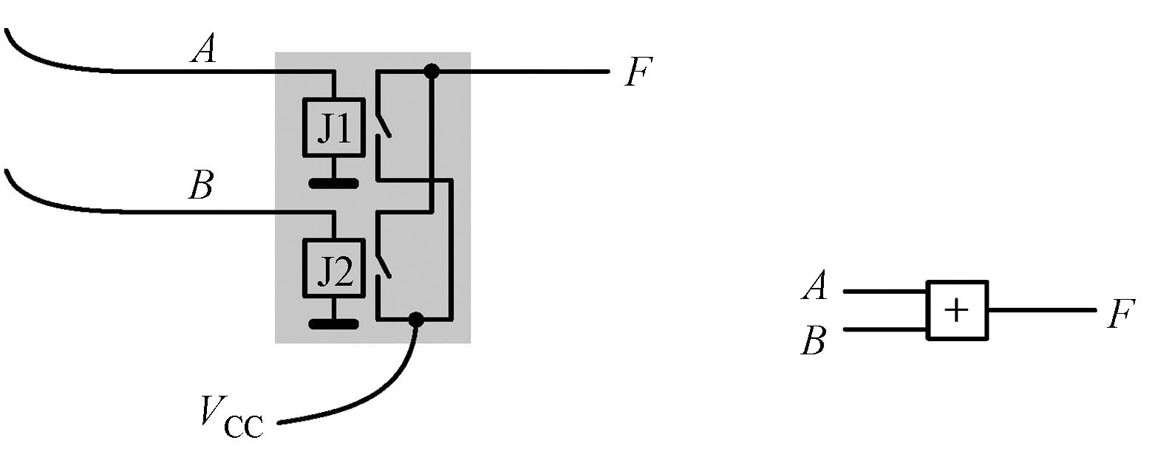
与非门
跟与操作结果相反。
真值表
| NAND | 0 | 1 |
|---|---|---|
| 0 | 1 | 1 |
| 1 | 1 | 0 |
符号
或非门
跟或操作相反。
真值表
| NOR | 0 | 1 |
|---|---|---|
| 0 | 1 | 0 |
| 1 | 0 | 0 |
符号
异或门
一个操作数为 1,另一个操作数为 0 时,结果才为 1。
真值表
| XOR | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
符号
电路图
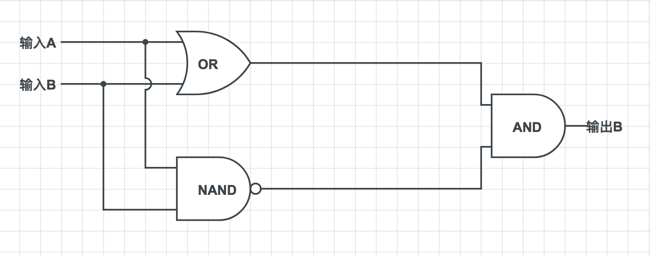
二进制加法器
计算二进制数加法与计算十进制数加法非常相似。如果你想让 245 和 673 这两个十进制数相加,你会把这个问题分解为几个简单的步骤。每个步骤只需要将两个十进制数相加,二进制加法也同理。
半加器和全加器
加法结果可以拆成两部分,一个是加和结果,另一个是进位结果。二进制加法也可以照下面这个方式进行拆分。
加和表
| +加和 | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
进位表
| +进位 | 0 | 1 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
可以利用两个逻辑门来实现上面的结果
异或门
| XOR | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
与门
| AND | 0 | 1 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 1 |
两个二进制数的加和结果是由异或门输出的,而进位结果是由与门输出的。因此我们可以将与门和异或门连接起来计算两个二进制数(即 A 和 B)的和。
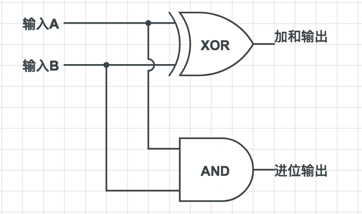
真值表
| 输入 A | 输入 B | 加和输出 | 进位输出 |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
这个被叫做半加器(Half Adder)。之所以被叫半加器是有原因的。它将两个二进制数相加,得出一个加法位和一个进位位。但是绝大多数二进制数是多于 1 位的。半加器没有做到的是将前一次的加法可能产生的进位位纳入下一次运算。例如,假设我们要将如下两个二进制数相加。
1111
+1111
-----
11110
我们只能将半加器用于最右面一列的相加:1 加 1 等于 0,进位 1。对于右面算起的第二列,由于进位位的存在,实际上需要将三个二进制数相加,而随后的每一列的加法都是这样的。随后的每一列二进制数相加都需要将进位位算进来。为了对三个二进制数进行加法运算你,我们需要将两个半加器和一个或门做如下连接。
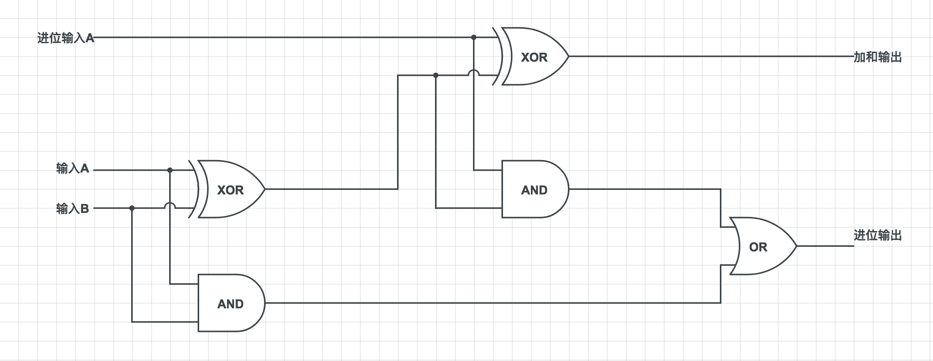
真值表
| 进位输入A | 输入A | 输入B | 加和输出 | 进位输出 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
这个叫做全加器(Full Adder)。我们用如下的符号表示它:

到这里,我们已经迈出了关键的第一步。因为我们可以利用它做 2 进制的加法:1+1=10!
多位二进制数相加
当然,只能进行一位二进制数相加的加法器的用途实在是太窄了,我们更需要能支持多位二进制数做加法的加法器。答案就是将多个全加器连接起来,组成多位加法器。假设我们将 4 个全加器连接起来,那么它就能做 4 位二进制数的加法。如下图所示:
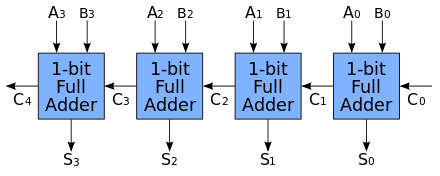
假设有两个 4 位二进制数 A₃A₂A₁A₀ 和 B₃B₂B₁B₀,只需要将它们按位相加,再逐级将低位的进位输出到高位进行计算即可。