统计学与生活

发表于 | 分类于
字数统计: 14k

一提起统计学，大家脑海中浮现的第一印象是什么？就我而言，我第一时间想到的就是那个著名的 抛硬币 实验。最近看了一本书，叫 《赤裸裸的统计学》，在里面发现了几个有趣的小故事，想与大家分享一下。

什么是概率

概率描述的是事件发生的可能性。

先来做两道判断题:

  • 天气预报说，明天有 99% 的概率会下雨，所以明天一定下雨。对吗？
  • 中国的 LOL 战队在 S8 赛季有 1% 的概率会夺冠，所以中国队在 S8 赛季不可能夺冠。对吗？

小结:

  • 再大概率的事件也有可能不发生
  • 再小概率的事件也有可能发生

蒙提霍尔问题

Q

在上个世纪的美国，有一个电视节目叫 “Let’s Make a Deal”，由当时极受欢迎的蒙提霍尔主持。在每天节目快要结束时，胜出的选手和蒙提霍尔都会站在 3 扇大门的前面。蒙提霍尔或告诉观众和选手，在其中一扇大门的门后会有一项大奖，如一辆小轿车，而另外两扇门的后面则各站着一头山羊。玩法很简单：选手选择一扇门，然后就会得到这扇门后面的奖品。

当选手和蒙提霍尔站在这 3 扇门的前面时，这位选手中大奖的概率为 1/3。但是，这档节目却有其微妙之处。当参赛者选定了一扇门，但未去开启它的时候，知道门后情形的蒙提霍尔会开启剩下两扇门的其中一扇，露出其中一只山羊。主持人随后会问参赛者要不要更换为另一扇关着的门？

这就是蒙提霍尔问题，如果换成是你，你又会怎么选呢？

A

答案是：当参赛者转向另一扇门而不是继续维持原先的选择时，赢得汽车的机会将会加倍!

三门问题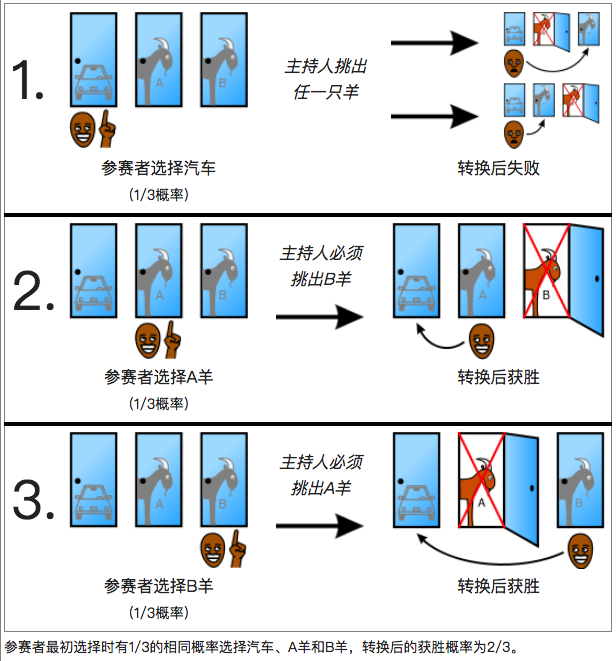

三门问题是多门问题里最难的情况。如果把三门变成千门，参赛者第一次就选中的概率就是 1/1000，参赛者就会清楚自己是在猜，而不是如同三门的时候 1/3 的概率认为自己是对的。这样，当主持人打开剩下 999 扇门中的 998 扇时，该如何选择，认真思考就会比三门的时候清晰很多。

施利茨啤酒广告

1981 年，美国约瑟夫·施利茨酿酒公司斥 170 万美元巨资为该公司旗下的旗舰品牌——施利茨啤酒开展了一场大胆而冒险的市场营销活动。当美国橄榄球超级杯大赛(即『超级碗』)的中场休息时间一到，施利茨公司就会当着全球亿万电视观众的面，现场直播一场别开生面的啤酒品鉴会，而挑选的对手不是别人，正是施利茨的死对头——米切罗啤酒。更让人大跌眼镜的是，参加品鉴会的不是别人，正是 100 名米切罗啤酒的忠实用户。这样的广告从始至终出现在季后赛的每一场比赛当中。类似的电视直播啤酒品鉴会总共有 5 场，每场都会邀请 100 名某品牌啤酒的『拥趸』，包括百威、米勒、米切罗等，让这些啤酒爱好者在自己最钟爱的啤酒和施利茨啤酒之间进行『盲品』。

广告噱头很明确：即使是那些自认为喜欢另一种品牌的啤酒爱好者，在盲品时也会发现自己更偏爱施利茨啤酒。啤酒公司甚至还请了一位橄榄球职业联赛的前裁判来监督整个活动过程。考虑到在数量众多的电视观众面前举办这样一场充满风险的啤酒品鉴会，你肯定会觉得施利茨啤酒的口感一定特别好，否则哪会有勇气搞这样的宣传，是吗？

让我们假设，要让施利茨公司满意，100 位盲品者中至少要有 40 位选择施利茨啤酒。这是一个非常可观的数字，因为所有参加盲品直播的人都曾信誓旦旦地声明自己是米切罗的忠实用户。而要达到这样的效果，其实一点儿都不难。施利茨只需要保证以下两点，那么他的计谋很大概率上就能成功：

  • 施利茨生产出的啤酒与其它品牌的啤酒在盲品时没有明显区别
  • 每场盲品的用户数量较多

这样一来，盲品结果就如抛硬币实验的结果一样，运用概率学的基本知识，就能得出至少有 40 人选择施利茨的概率为 98%，至少有 45 人选择施利茨的概率为 86%。从理论上来看，这场电视营销活动其实并没有很大的风险。

那么这 98% 和 86% 的概率是怎么计算出来的呢？不要着急，我们接着往下看。

相关事件和独立事件

我们在生活中时常会遇到随机事件。抛硬币、掷骰子、刮奖彩票等都是随机事件。你要学会区分哪些随机事件是属于独立事件，哪些随机事件是属于相关事件。

  • 相关事件，上一个事件会影响到下一个事件
  • 例，从布袋里不放回地拿玻璃球。每拿走一颗玻璃球，袋子里就少一颗玻璃球，概率也随之改变。
  • 独立事件，不受过去事件的影响
  • 例，抛硬币。硬币不知道它曾经是正面向上还是反面向上。所以每一次抛掷硬币的结果都是独立事件。

赌徒谬误

我们先来看一下抛硬币的例子。抛掷一枚硬币，出现正面和反面的概率各 0.5，抛掷第 1 次，结果为正面的概率为 0.5。那么抛掷第 2 次和抛掷第 3 次，结果为正面的概率是多少呢？还是 0.5。

有些人可能想：『已经三次正面了，这一次应该轮到反面了吧』。其实不然，下一次抛掷为正面的概率依然是 0.5。

独立事件的概率

两个或多个独立事件同时发生的概率是每个事件概率的乘积。

掷 1 次可能出现的结果有 2 个，正、反。因为 p=0.5，所以每个结果出现的概率是 0.5，那么正面出现 1 次、0 次的概率为 0.5、0.5。

掷 2 次可能出现的结果有 4 个，正正、正反、反正、反反。每个结果出现的概率是 0.5×0.5=0.25，那正面出现 2 次、1 次、0 次的概率分别是 0.25、0.5、0.25。

掷 3 次可能出现的结果有 8 个，正正正、正正反、正反正、正反反、反正正、反正反、反反正、反反反。每个结果出现的概率是 0.5×0.5×0.5=0.125，那正面出现 3 次、2 次、1 次、0 次的概率分别是 0.125、0.375、0.375、0.125。

但如果我们抛了 100 次硬币，这个时候又该如何计算每个结果出现的概率呢，难道要一一列举出来吗。结果的概率计算有规律吗?有的。

假设

  • p 是我们预期事件发生的概率(正面向上)
  • k 是我们预期事件发生的次数(0≤k≤n)
  • 总共进行了 n 次实验

所以，每个结果出现的概率就是 $$ p^k(1-p)^{n-k} $$

排列与组合

  • 排列，对选出来元素的顺序有要求
  • 例，从 3 到 9 共计 7 个号码球，从中选三个号码球用来组成一个三位数，请问可以组成多少个三位数？百位数有 7 种可能，十位数有 (7-1) 种可能，个位数有 (7-1-1) 种可能，共计有 210=7*6*5 种排列。即 $$ A_7^3 = \frac{7!}{(7-3)!} $$
  • 组合，对选出来元素的顺序无要求
  • 例，从 3 到 9 共计 7 个号码球，从中选三个号码球用来炸金花，请问有多少种组合？假设你扎金花的时候拿到了三张牌 345，那么无论你排成 345 354 435 453 534 543，大家都会认为它是同一个顺子。所以这里计算的话需要多一个去重的步骤。共计有 35=7*6*5/3*2*1 种组合。即 $$ C_7^3 = \frac{7!}{(7-3)!3!} $$

二项分布

什么是二项分布

  • 每次试验是独立事件
  • 每次试验只有两个可能的结果
  • 每次试验中成功的概率是不变的

二项分布的概率计算公式

$$P(n取k)=\frac{n!}{(n-k)!k!}p^k(1-p)^{n-k}$$

举个例子

  • 求抛掷 3 次硬币时，只有两个正面向上的硬币的概率为多大？
  • 将 n=3，p=0.5，k=2，带入得到每个结果的发生的概率为 $$p=0.5^2(1-0.5)^{3-2}=0.125$$
  • 那么该结果出现的次数是 $$ C_3^2=\frac{3!}{(3-2)!2!}=3$$

所以，P(3取2)=3×0.125=0.375

再回到我们的施利茨啤酒广告，$$P(至少要有40位选择施利茨啤酒)=P(40)+P(41)+…+P(100)\approx 0.982$$ $$P(至少要有45位选择施利茨啤酒)=P(45)+P(41)+…+P(100)\approx 0.864$$

P(x>=40)

P(x>=45)

生活中还有哪些与统计学相关的有趣故事呢？欢迎大家在下方留言。

附 计算 P(x) 的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
package statistics;

import java.math.BigDecimal;

/**
 * 二项分布
 * <p>
 * 这里计算的是 p=0.5 的情况。
 */
public class BinomialDistribution {

    /**
     * 在 n 次实验中，预期的结果次数 = x 次的概率
     *
     * @param n
     * @param x
     * @return
     */
    public static BigDecimal equals(int n, int x) {
        //n!
        BigDecimal nFactorial = new BigDecimal(1);
        //(n-x)!
        BigDecimal nSubxFactorial = new BigDecimal(1);
        //临时值
        BigDecimal temp = BigDecimal.ZERO;
        //结果值
        BigDecimal result = BigDecimal.ZERO;
        for (int i = n; i > x; i--) {
            nFactorial = nFactorial.multiply(new BigDecimal(i));
        }
        for (int i = (n - x); i > 0; i--) {
            nSubxFactorial = nSubxFactorial.multiply(new BigDecimal(i));
        }
        temp = nFactorial.divide(nSubxFactorial);
        //这里计算的是 p 的概率为 1/2 的二项分布
        for (int i = n; i > 0; i--) {
            temp = temp.divide(new BigDecimal(2));
        }
        result = temp;
        return result;
    }

    /**
     * 在 n 次实验中，预期的结果次数 < x 次的概率
     *
     * @param n
     * @param x
     * @return
     */
    public static BigDecimal lessThan(int n, int x) {
        BigDecimal result = BigDecimal.ZERO;
        for (int i = (x - 1); i > 0; i--) {
            result = result.add(equals(n, i));
        }
        return result;
    }

    /**
     * 在 n 次实验中，预期的结果次数 >= x 次的概率
     *
     * @param n
     * @param x
     * @return
     */
    public static BigDecimal moreThan(int n, int x) {
        BigDecimal result = BigDecimal.ZERO;
        for (int i = x; i < n; i++) {
            result = result.add(equals(n, i));
        }
        return result;
    }

    public static void main(String[] args) {
        int n = 100;//总的实验次数
        int x = 40;//预期的结果次数
        System.out.println("P(x=" + x + ") = " + equals(n, x));
        System.out.println("P(x<" + x + ") = " + lessThan(n, x));
        System.out.println("P(x>=" + x + ") = " + moreThan(n, x));
    }
}

引用