浮点数在计算机中的表示

发表于 | 分类于
字数统计: 15k

现实世界中不仅有整数，还有小数，有没有一种编码，能同时表示它们呢。IEEE 754 是 20 世纪 80 年代以来最广泛使用的浮点数运算标准，为许多 CPU 与浮点运算器所采用，简单来说，它采用了类似科学记数法的形式来表示整数和小数。该标准的设计者，William Morton Kahan 教授在 1989 年获得图灵奖。

产生背景

因为 定点数 存在两个缺陷

  • 不能有效的表示非常大的数字。
    • 例如，表达式 \( 5\times2^{100}\) 是 \((101)_2\) 后面跟着 100 个零的位模式来表示，如果用定点表示法，容易产生溢出。
  • 不能有效的表示小数。

为了解决上述问题，浮点数应运而生。

表示方法

科学记数法

参照科学记数法，IEEE 浮点标准采用如下形式来表示一个数(Value)

$$V = (-1)^s \times M \times 2^E$$

  • \((-1)^s\) 表示符号位，当 s=0， V 为正数；当 s=1，V 为负数。
  • M 表示有效数字，范围属于 [1,2)。
  • \(2^E\) 表示指数位。

例 1
十进制的 5.0 写成二进制是 101.0，相当于 \((1.01)\times2^2\)。按照上面的格式，可以得出 s=0，M=1.01，E=2。

有效数字 M

因为 \(1 \le M < 2\)，也就是说，M 的整数部分总是为 1，所以我们可以只保留它的小数(fraction)部分，而将开头的 1 省略。这样一来，就能多表示一位有效数字。

  • 在单精度浮点格式中，s、exp、fraction 字段分别为 1、8、23 位。
  • 在双精度浮点格式中，s、exp、fraction 字段分别为 1、11、52 位。

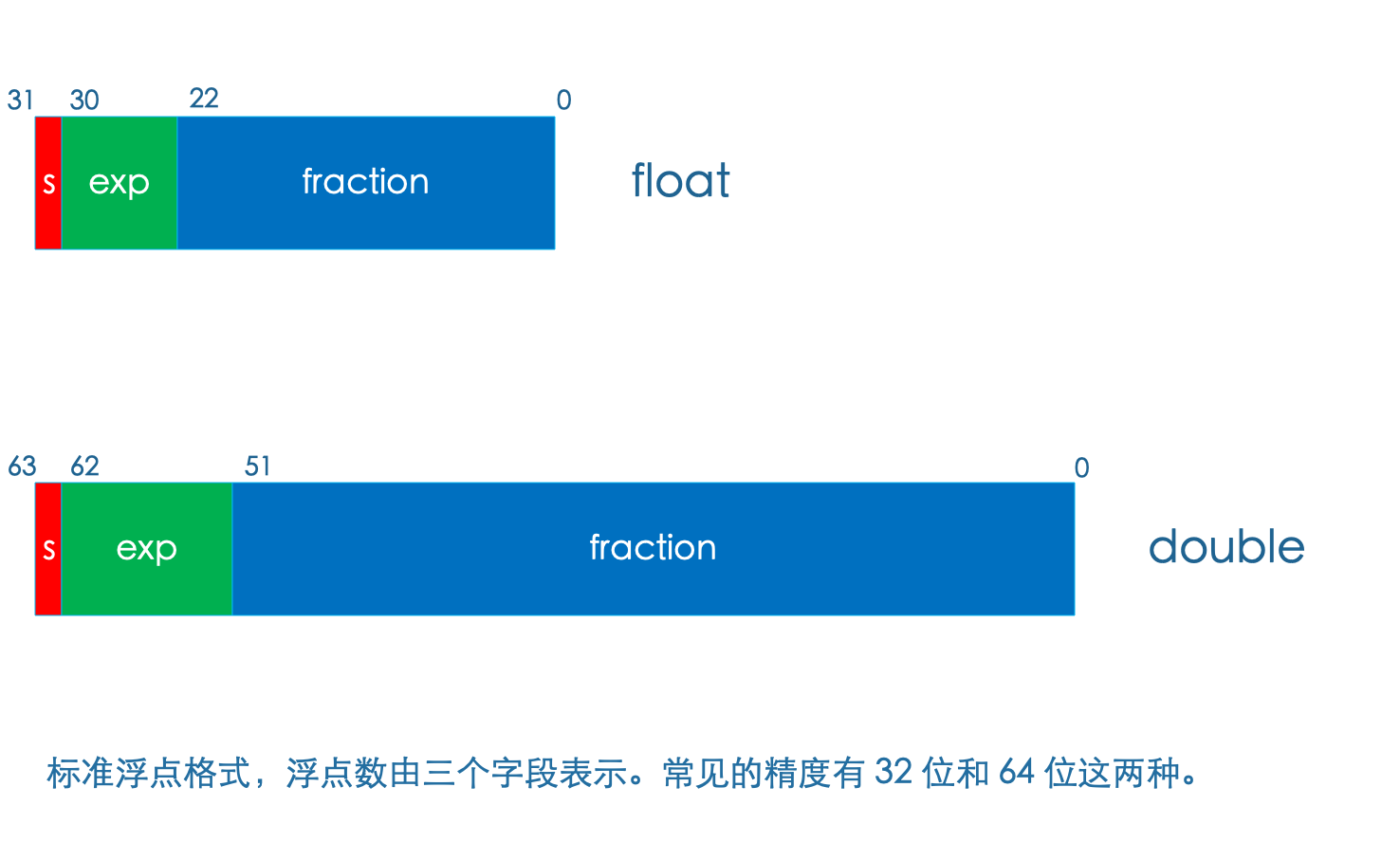
指数 E

指数 E 的取值情况比较复杂，我们以 float 浮点类型为例。

  • 当 exp 既不全为 0，也不全为 1 时
    • E = exp - 127。\(这里的;127;是一个偏置值;=;2^7-1\)。 \(有效数字;M=1+fraction。\)
  • 当 exp 全为 0 时
    • E = 1 - 127。\(有效数字;M=fraction,;不用在前面加上;1\)。特别的，当 fraction 全为 0 时，表示 \(\pm0\) (取决于符号位)。
  • 当 exp 全为 1 时
    • 如果 fraction 全为 0，表示 \(\pm\infty\) (取决于符号位)。
    • 如果 fraction 不全为 0，表示 NaN (Not a Number)。

精度问题

十进制和二进制相互转化

先看看十进制数和二进制数如何相互转换。用下标表示数的基，\(d_{10}\) 表示十进制数，\(d_2\) 表示二进制数。

一个具有 n+1 位整数，m 位小数的十进制数 \(d_{10}\) 表示为

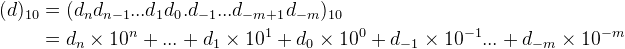
例 2

$$ (1234.5678)_{10} = 1\times10^3 + 2\times10^2 + 3\times10^1 + 4\times10^0 + 5\times10^{-1} + 6\times10^{-2} + 7\times10^{-3} + 8\times10^{-4}$$

同理，一个具有 n+1 位整数 m 位小数的二进制数 \(b_2\) 表示为

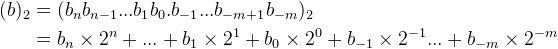
例 3

$$ (1010.1001)_2 = 1\times2^3 + 0\times2^2 + 1\times2^1 + 0\times2^0 + 1\times2^{-1} + 0\times2^{-2} + 0\times2^{-3} + 1\times2^{-4} $$

将二进制数转换成十进制数，比较容易，如例 3 所示。而将十进制数转换成二进制数，需要把整数部分和小数部分分开转换，整数部分用 2 除，取余数；小数部分用 2 乘，取整数位。

例 3
把 \((13.125)_{10}\) 转换成二进制数。

整数部分: \( (13)_{10} = (1101)_2 \)
\((1);13\div2=6 ; 余数为;1 \Rightarrow 1 \)
\((2);6\div2=3 ; 余数为;0 \Rightarrow 01 \)
\((3);3\div2=1 ; 余数为;1 \Rightarrow 101 \)
\((4);最后得到的商小于;2，;所以不用再继续除了。 \Rightarrow 1101 \)

小数部分: \( (0.125)_{10} = (001)_2 \)
\((1);0.125\times2=0.25 ;整数位是;0 \Rightarrow .0 \)
\((2);0.25\times2=0.5 ;整数位是;0 \Rightarrow .00 \)
\((3);0.5\times2=1.0 ;整数位是;1 \Rightarrow .001 \)
\((4);最后得到的乘积是个整数，所以不用再继续乘了。\)

所以 \( (13.125)_{10} = (1101.001)_2 \)。

一个十进制数能否用二进制浮点数精确表示，关键在于小数部分。 我们来看一个最简单的小数 \((0.1)_{10}\) 能否精确表示。
\((1);0.1\times2=0.2;整数位是;0 \Rightarrow .0\)
\((2);0.2\times2=0.4;整数位是;0 \Rightarrow .00\)
\((3);0.4\times2=0.8;整数位是;0 \Rightarrow .000\)
\((4);0.8\times2=1.6;整数位是;1 \Rightarrow .0001\)
\((5);0.6\times2=1.2;整数位是;1 \Rightarrow .00011\)
\((6);0.2\times2=0.4;整数位是;0 \Rightarrow .000110 \ 由第(2)步开始循环。\)
…

我们得到一个无限循环的二进制小数 \((0.1)_{10}=(0.0;0011;0011;0011;…)_2\)。

用有限位无法表示无限循环小数，因此，\((0.1)_{10}\) 无法用 IEEE 754 浮点数精确表示。同时我们还可以得出

\((0.2)_{10} = (0.0011;0011 …)_2\)

\((0.4)_{10} = (0.0110;0110 …)_2\)

\((0.6)_{10} = (0.1001;1001 …)_2\)

\((0.8)_{10} = (0.1100;1100 …)_2\)

这四个数也无法精确表示。同理

\((0.3)_{10}\times2 = 0.6 \)

\((0.7)_{10}\times2 = 1.4 \)

\((0.9)_{10}\times2 = 1.8 \)

这三个数也无法精确表示。 所以，从 0.1 到 0.9 这 9 个小数中，只有 0.5 可以精确表示

\((0.5)_{10} = (0.1)_2\)

二进制小数能精确表示的十进制小数的基本规律

一个十进制小数要能用浮点数精确表示，最后一位必须是 5，因为 1 除以 2 永远是 0.5。当然，这是必要条件，并非充分条件。

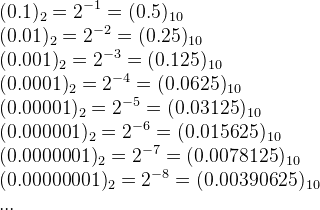
一个 m 位二进制小数能够精确表示的小数有多少个呢？

当然是 \(2^m\) 个。而 m 位十进制小数有 \(10^{m}\)个，因此，能精确表示的十进制小数的比例是 \(\frac{2^m}{10^{m}}=(0.2)^{m}\)。m 越大，比例值越小。

其实不管是用十进制、二进制或者其它进制，都存在着有限位数无法精确表示的数字。这时候就需要进行舍入。

舍入

IEEE 标准列出 4 种不同的舍入方法

  • 最近舍入
    • 舍入到最接近，在一样接近的情况下偶数优先（Ties To Even，这是默认的舍入方式）。
  • 朝 \(+\infty\) 方向舍入
  • 朝 \(-\infty\) 方向舍入
  • 朝 0 方向舍入

代码验证

show-byte.c

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include<stdio.h>
#include<string.h>

/*
C 语言中的 typedef 声明提供了一种给数据类型命名的方式。这能够极大地改善代码的可读性，因为深度嵌套的类型声明很难读懂。
typedef 的语法与声明变量的语法十分相像，除了它使用的是类型名，而不是变量名。

1 typedef int *int_pointer;
2 int_pointer ip;
3 int *ip;

2，3 行中的定义是等价的。
*/

typedef unsigned char * byte_pointer; //用 byte_pointer 声明和用 unsigned char * 声明效果是相同的。

void show_bytes(byte_pointer start, size_t len) {
	size_t i;
	for(i=0; i<len; i++) {
		printf("%.2x", start[i]);
	}
	printf("\n");
}

int main() {
	float f1=1.1;
	printf("\nf1 = %0.1f\n", f1);
	show_bytes((byte_pointer)&f1, sizeof(f1));
	double d=1.1;
	show_bytes((byte_pointer)&d, sizeof(d));

	float f2=1.3;
	printf("\nf2 = %0.1f\n", f2);
	show_bytes((byte_pointer)&f2, sizeof(f2));
	double d2=1.3;
	show_bytes((byte_pointer)&d2, sizeof(d2));

	float f3=1.7;
	printf("\nf3 = %0.1f\n", f3);
	show_bytes((byte_pointer)&f3, sizeof(f3));
	double d3=1.7;
	show_bytes((byte_pointer)&d3, sizeof(d3));

	float f4=1.9;
	printf("\nf4 = %0.1f\n", f4);
	show_bytes((byte_pointer)&f4, sizeof(f4));
	double d4=1.9;
	show_bytes((byte_pointer)&d4, sizeof(d4));
}

little-big-endian

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include <stdio.h>

int main() {
	int i = 0x11223344;
	char *p;

	p = (char *) &i;
	if (*p == 0x44) {
		printf("little endian\n");
	}else if(*p == 0x11) {
		printf("big endian\n");
	}
	return 0;
}

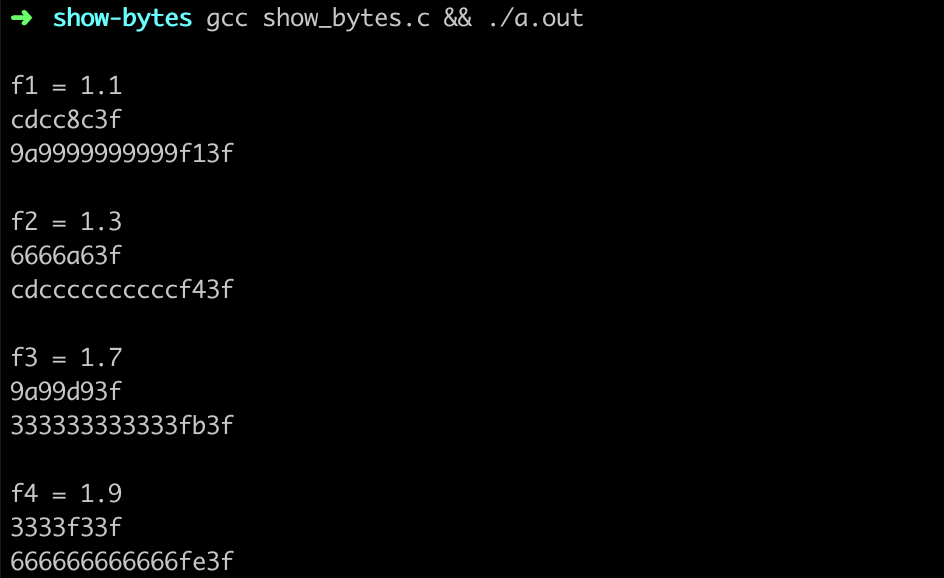
我的电脑是 小端序，最低位先输出。

\((1.1)_{10}\)

  • \((3f8ccccd)_{16} = (0011;1111;1000;1100;1100;1100;1100;1101)_2\)

    • 符号位 S = 0
    • 指数 E = exp-127 = 127-127 = 0
    • 小数部分 = \(000;\overline{1100}\)
    • 有效数字 M = 1.000 1100 1100 1100 1100 1101
    • 舍入 \(11\Rightarrow1\)
    • \(Value = (-1)^0\times(1.000;1100;…;1101)\times2^0 = 1.000;1100;1100;1100;1100;1101\)

  • \((3ff99999999999a)_{16} = (0011;1111;1111;0001;1001;1001;…;1001;1010)_2\)

    • 符号位 S = 0
    • 指数位 E = exp-1023 = 1023-1023 = 0
    • 小数部分 = \(0001;\overline{1001}\)
    • 有效数字 M = 1.0001 1001 1001 1001 … 1010
    • 舍入 \(10\Rightarrow1\)
    • \(Value = (-1)^0\times(1.0001;1001;…;1010)\times2^0 = 1.0001;1001;1001;…;1001;1010\)

\((1.3)_{10}\)

  • \((3fa66666)_{16} = (0011;1111;1010;0110;0110;0110;0110;0110)_2\)

    • 小数部分 = \(010;\overline{0110}\)
    • 舍入 \(01\Rightarrow0\)

  • \((3ff4cccccccccccd)_{16} = (0011;1111;1111;0100;1100;1100;…;1100;1101)_2\)

    • 小数部分 = \(0100;\overline{1100}\)
    • 舍入 \(11\Rightarrow1\)

\((1.7)_{10}\)

  • \((3fd9999a)_{16} = (0011;1111;1101;1001;1001;1001;1001;1001)_2\)

    • 小数部分 = \(101;\overline{1001}\)
    • 舍入 \(10\Rightarrow1\)

  • \((3ffb333333333333)_{16} = (0011;1111;1111;1011;0011;0011;…;0011;0011)_2\)

    • 小数部分 = \((1011;\overline{0011})\)
    • 舍入 \(00\Rightarrow0\)

\((1.9)_{10}\)

  • \((3ff33333)_{16} = (0011;1111;1111;0011;0011;0011;0011;0011)_2\)

    • 小数部分 = \(111;\overline{0011}\)
    • 舍入 \(00\Rightarrow0\)

  • \((3ffe666666666666)_{16} = (0011;1111;1111;1110;0110;0110;…;0110;0110)_2\)

    • 小数部分 = \((1110;\overline{0110})\)
    • 舍入 \(01\Rightarrow0\)

拓展

Q1

为什么 exp 需要加上一个偏置值？

A1

采用这种方式表示的目的是简化比较。因为，指数的值可能为正也可能为负，如果采用补码表示的话，符号位 S 和 Exp 自身的符号位将导致不能简单的进行大小比较。正因为如此，指数部分通常采用一个无符号的正数值存储。

引用